The tallest man to ever live was Robert Wadlow, who reached a staggering 2.72m. That’s equal to a very large male ostrich or Shaquille O’Neal with two bowling pins balanced on his head.
Wadlow had a condition that caused excessive growth. These conditions are often corrected, so it’s unlikely anyone will ever reach these heights again.
But could evolution change this?
Humans have been getting taller. In the last 175 years, the average height of Australian males has increased by 8.4cm.
Are we evolving to be taller? Will our average height plateau out? Could we theoretically continue to grow taller and larger? What are our limits?
To find answers to these increasingly existential questions, I sought solace in a mathematician, Stephen Woodcock.
An associate professor of applied mathematics at the University of Technology Sydney, Stephen turned out to be the perfect man for the job because he was willing to try to lift a 75kg person on his toes to understand pivot points.
This was – I’m told – a necessary but painful step (pun intended) to determine how long a human foot could get before we couldn’t walk any more.
TAKE A WALK
So how long could a human foot get before it could no longer be lifted?
Let’s imagine a simple model of a human foot and ankle, where the foot is a horizontal block, the ankle is a pivot point and the leg is a vertical rod.
Like all maths, we need to make some assumptions.
Stephen says we need to assume the centre of mass of an average foot is in the middle. We also need to assume the ankle is at the very back of our feet, which isn’t strictly the case, but it’s pretty close.
A standard human foot weighs about 1.2kg and is 30cm long. If your foot was 1m long, it would be 4kg. Basically, an average foot weighs 4kg/m.
“I realise kilos per metre is a weird unit of foot density,” says Stephen.
“This also assumes the foot remains the same width and doesn’t get any wider.”
Then we need to calculate the maximum moment – the rotational effect from a force. In this case, the moment refers to the rotation in your ankle.
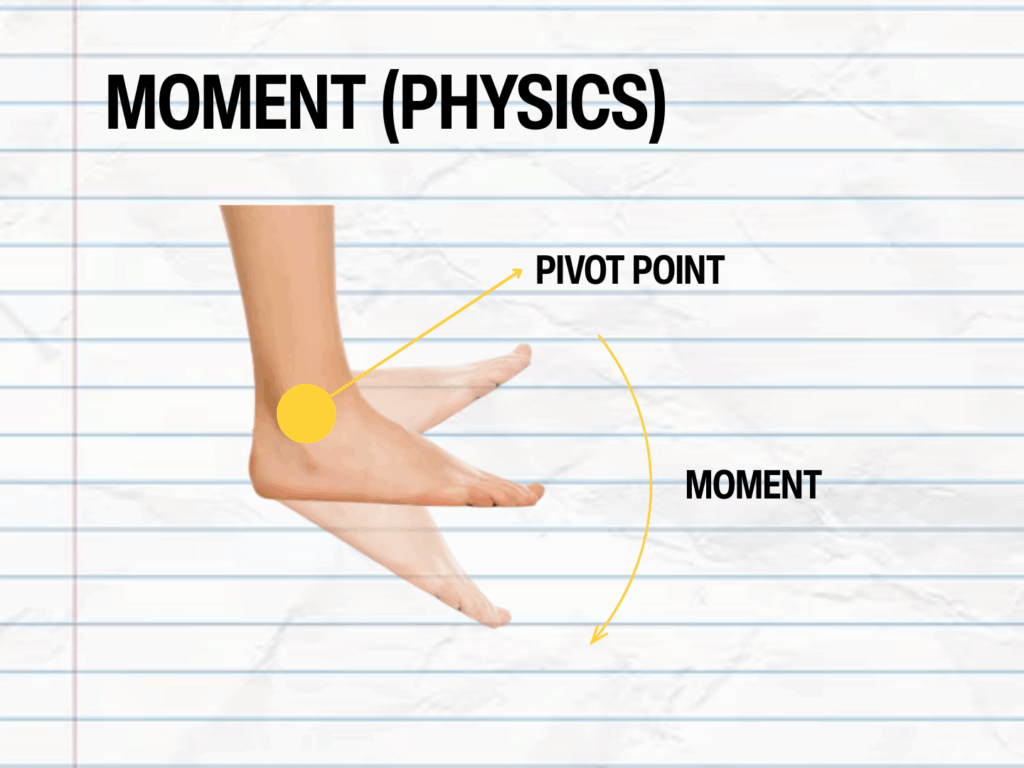
Credit: Cat Williams
“Most people have used a lever or a crowbar or a knife to jam open a jar,” says Stephen.
“The further you are from the thing you’re trying to move, the more force you can get.”
To calculate the maximum moment – the maximum rotation your foot can endure – Stephen got creative, doing the “oh-so-scientific test of asking someone to stand on my toes,” he says.
Why did he get people to stand on his feet?
“I needed an order of magnitude,” he says. Like it was obvious.
He needed to understand what the maximum mass on his feet he could lift would be while still being able to walk.
“If someone stood on your toes – about 30cm from the pivot – I could just about lift up about a 75kg person standing on my toes. It’s bloody painful but I can just about get my ankle to actually lift that.”
“Somebody with a stronger ankle could obviously lift a longer foot than someone with a weaker ankle.”
Now that Stephen’s toes are sufficiently sore, we solve for 75kg (maximum liftable mass) times by 0.3m (distance between ankle and toes of an average foot) times by 10 newtons per kilogram (N/kg). This 10N/kg is to account for gravity, as every kilogram of mass on Earth experiences roughly 10 newtons of gravitational force by simply existing.
You get 75kg x 0.3m x 10N/kg = 225Nm. Therefore, the total moment an average ankle can withstand is 225 newton-metres.
The maximum liftable foot length (L) must be 225Nm = (4kg x L) x (L/2)m x 10N/kg.
In this equation, the 225Nm is the total force an ankle can withstand, (4kg x L) is the average weight of a foot per metre times the unknown foot length, (L/2)m is the location of the centre of mass along the unknown foot length and 10N/kg is the gravity factor.
Some maths (on Stephen’s behalf) finds the maximum length a human foot could be before you couldn’t lift it is 3.35m.
That’s a very long foot and much longer than I anticipated would be mathematically possible. It’s also 2.88m longer than one of Robert Wadlow’s feet.
“Even skis for example, which are long but not that long, they’re much lighter than bone and tissue,” says Stephen. “A ski does not weigh as much as human flesh.”
Of course, Stephen says there are plenty of other factors to consider, like if your foot was floppy from the half-way point and couldn’t hold up your hypothetically massive toes. We need to assume strong muscles and strong bones all the way along this foot.
“Good luck buying shoes,” says Stephen.
So if we can have enormous feet, would they be in proportion with our potential maximum height?
REACHING NEW HEIGHTS
Again, there’s a few things to consider before we leap into any calculations.
“The biggest barrier here is probably the square-cube law,” says Stephen.
If we decided to increase our size by double, then we would get doubled in all dimensions.
“Doubling your size increases the cross-sectional area four-fold, because you’re twice as long and twice as wide, so you’ve got four times the cross-section,” says Stephen.
“But your mass is related to the volume that you are. So if you’re twice as wide and twice as long and twice as tall, you’re eight times the volume.
“You’re two times two times two.”

Credit: Morgan Knoxlee, overlay Cat Williams
For example, if I was doubled in all dimensions, I would become 3.34m tall, 1m wide and 0.5m deep. I would be eight times heavier (520kg) and my cross-section would be four times larger. This cross-section is the area of your body if you were chopped in half.
The problems don’t stop there though – the stress on my bones and joints would also be doubled.
“If you are twice as big in every dimension, all of your joints and all of your bones are carrying twice as much strain as they would be otherwise,” says Stephen.
“If you simply made everyone a giant by increasing in all dimensions, then you would soon get issues with your neck giving way or your collarbone snapping too easily.”
This square-cube law is the reason a flea can jump much higher than itself but an elephant can’t.
We don’t want to stretch someone in all dimensions, just their height.
Unfortunately, maths isn’t our height’s limiting factor. It’s more of a matter of biology.
The extreme blood pressure needed to move blood around the body of someone very tall could rupture blood vessels.
“The flip side of the square-cube law,” Stephen says, “is larger pressure is needed, but [there’s] no increase in tissue strength.”
Sultan Kösen is the tallest living person at 2.51m tall (8ft 2.82in). He has issues with high blood pressure, but luckily not so high to cause fatal implications. Robert Wadlow wasn’t so lucky.
Anyone over 9ft tall would be expected to experience blood pressure so extreme their blood vessels would burst, killing them fairly quickly. (Hopefully at least before they fall 9ft to the ground below.)
Unless we evolve a way to strengthen our blood vessels, it seems our average height won’t be sky rocketing any time soon.
WHERE ARE WE HEADING?
If our feet could grow longer than our maximum theoretical height, where does that leave the proportions of the rest of our body?
I asked Stephen about the maximum theoretical size of the human head. Unsurprisingly, we must start with the neck.
“Human neck strength varies enormously,” says Stephen.
One paper suggests neck strength varies between 15 and 223 newtons in women and between 38 and 383 newtons in men.
For now, we’re back to assumptions. Stephen says we need to assume the head is spherical and of a uniform density, meaning the centre of mass is bang in the middle and the neck connects directly under this centre of mass.
“In reality, your neck is generally behind the centre of mass but, hey, if we’re allowing heads to grow like Pixar characters, then we can also have the necks in somewhat cartoon-y placements,” says Stephen.
The next step is assessing how dense we are.
“The density of a human head is very close to that of water,” says Stephen.
“It’s about 1 tonne per cubic metre, not that you could have a cubic metre or a tonne of head.”
Basically, our head weighs 1kg per 0.001 cubic metres.
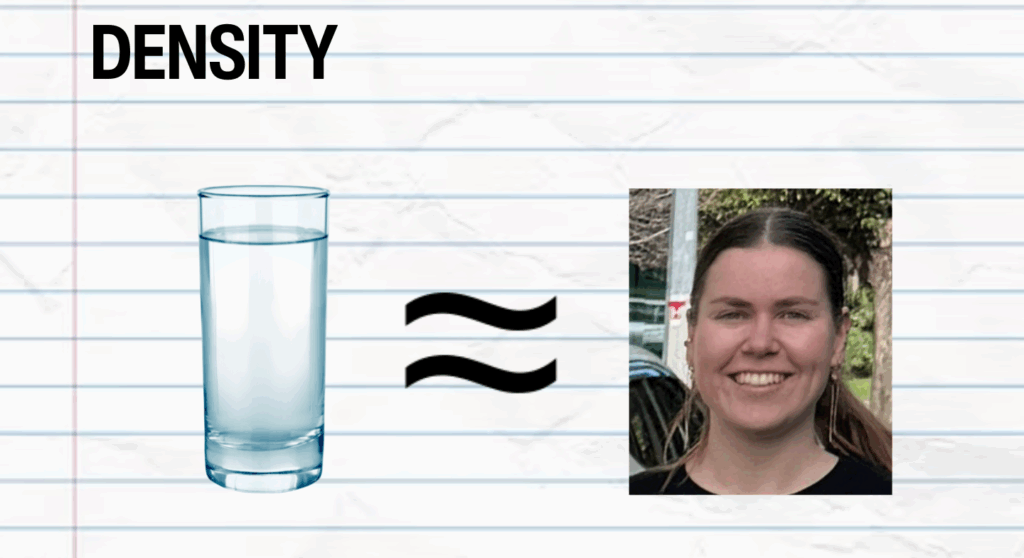
Credit: Cat Williams
Given I have no way of testing it, I’m going to assume my neck strength is 200N. A neck strength of 200N is the equivalent of being able to hold up 20kg.
At a density of 0.001 cubic metres per kilogram of head, my hypothetical spherical head volume would be 0.020 cubic metres.
The volume of a sphere is (4/3) times by pi (π) times by the radius to the power of three.
We need to solve the following: 0.02 = (4/3) x π x r3, where r is the radius of my hypothetical huge head.
The solution gives a radius of 17cm, so the diameter of my head would be 34cm. Compared to my enormous feet, this seems fairly small.
Stephen imagined a watermelon to make it seem larger. It worked because envisioning a 34cm round watermelon atop my neck hurts just thinking about it.
“Having that [watermelon] on your head would not just be a poor fashion choice, rather a literal pain in the neck,” he laughs.

Credit: Morgan Knoxlee
ONWARDS AND UPWARDS
Where will evolution take us?
Could we mathematically continue to grow taller and taller, get increasingly longer feet and enormous watermelon-sized heads?
With so many factors to consider, there isn’t a particularly straightforward answer.
“We’ve had evolution and speciation for millennia,” says Stephen.
“If you rewound back to … a hairy ancestor with a tail, would you have expected that this creature would have abandoned whichever tree it lived in, started shaving, gotten a mortgage and become more like you or me?”
Probably not, but Stephen thinks we have reached a plateau in terms of our order of magnitude. In other words, it appears we’re at our best and most efficient ‘size to fleshiness ratio’.
“I would imagine that, given it’s not just humans which have hit this size to fleshiness ratio, we probably are in the realm of where we’re meant to be,” says Stephen.
“A gorilla is larger than either of us are going to be.
“But it’s still the same order of magnitude. It’s still made out of mammal bones and flesh and skin.
“Sure, they’ve got bigger arms, bigger legs and hairier bums, but … there is at least an order of magnitude which everything seems to stick to.”
I brought up the Neanderthals as a counter argument to our current order of magnitude, because I don’t want to believe we won’t all become giants one day.
Stephen says they’re still all the same materials. Mammal bones and flesh and skin.
“If you rewound 1000 years … a lot of [limited growth] was nutrition based, where people were 10–20cm shorter than they were nowadays, but that’s [only] 10cm shorter,” says Stephen.
For now, we’re probably right about where humans are meant to be.
“Who on Earth knows in the wholeness of time?” says Stephen.
That is to say, take all of this with a very large grain of salt.









